1. Blackjack Best Betting Strategy
  2. Optimal Craps Betting Strategy
  3. Blackjack Betting Guide
  4. Best Blackjack Betting Strategy Reddit

About Blackjack

Blackjack is the most well known and most popular casino game available. Even movies have been made around the game of blackjack. It has pretty simple objective and basic rules – player plays against banker and tries to get closer to a sum of 21 than banker but not exceed it. Banker has certain limitations which strategy it has to follow but player has to act before banker.

Blackjack Rules

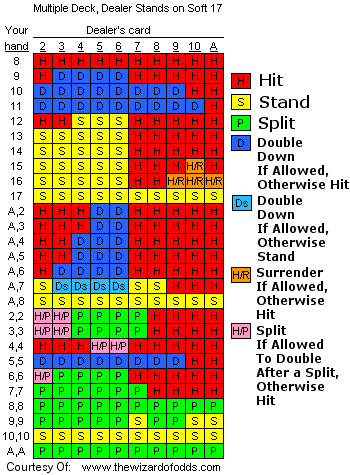
Blackjack should need no introduction. It is the most popular table game in the United States, and is easily found in casinos throughout the world. The object of the game of Blackjack is simply to get more points than the dealer without going over 21. Rules Hand Signals Wizard’s Simple Strategy Basic Strategy Blackjack. If the player wins, they make that same small bet again. If they lose, they instead double their bet. If the player loses again, they double their bet again. The player continues doubling their bet until they win, at which point they revert to their original small bet size.

Blackjack is a card game played with between 1 to 8 standard decks of playing cards. Cards are shuffled and placed to a so called “shoe”, where they are then dealt from for each deal. At online casinos, the shoe is shuffled after each hand at most cases. Cards of rank between 2 to 10 are valued at their face value and all the face cards are valued as 10. An ace is valued 1 or 11. The highest possible hand is an ace and any 10-point card. This is so called “blackjack”. A winning blackjack pays 3:2. The player wins if his hand has more points than the dealer, without going over 21 (busting). If both player and dealer have a blackjack or both have the same point value hand, the hand is a push. Aside from a blackjack, a winning hand pays 1:1. If player busts, dealer wins automatically that hand. If player has an ace in his hand, for example ace+6, he has so called “soft hand” (an ace is either a 1 or 11), meaning that he either has a sum of 7 (soft total) or 17 (hard total). If player draws a card which would make his hard total over 21, then the ace plays as a 1 the rest of the hand.

Gameplay

The Kelly Criterion is by far the most sophisticated and complex betting system which can be used in blackjack and other gambling games. It is based upon concepts of probability theory. The mathematics of the Kelly Criterion can be somewhat difficult to master, but the system has consistently outperformed other methods of betting since it was introduced.

1) After player has decided and placed a bet, the both player and dealer are dealt two cards. Dealers other card is face down and player´s both cards are dealt face up. If the dealer has an ace or 10-point card showing, he will peek for a possible blackjack (under standard online rules). If the dealer has an ace as a showing upcard, the player has an opportunity to buy “insurance” against the blackjack. If player decides to buy insurance and the dealer’s remaining card is a 10-point card forming a blackjack, then insurance bet pays 2:1. Under standard online rules, taking insurance is not profitable. The only situation when taking insurance is profitable is when:

Blackjack Best Betting Strategy

A) A shoe contains only 1 deck, player plays 3 hands at a time and there are no visible 10-point cards showing.

B) A shoe contains only 1 deck, player plays 5 hands at a time and there are 0 to 2 visible 10-point cards showing at the table.

C) A shoe contains 2 decks, player plays 5 hands at a time and there are 0 visible 10-point cards showing at the table.

Usually online blackjack is played with 4 to 8 decks, so taking insurance is not profitable if player likes to follow optimal strategy.

Some online casino also offer “even money” bet, if player has a dealt blackjack and dealer has an ace showing. This bet also pays 2:1, but is never profitable, if player likes to follow optimal strategy.

2) Now if the dealer does have a blackjack, the hand will end. If the dealer does not have a blackjack, then the player has a few options to choose from what to do with his hand:

Stand: The player can keep his current two cards, not taking more giving turn to the dealer.

Hit: The player can take one or more cards to his hand. The player can continue hitting until reaching 21 or busting.

Double: The player can double his bet and take one another card. The player is not allowed to hit after a double and can only double on a 2-card hand.

Split: If the player has two cards of equal rank, he can split the cards into two separate hands. The bet is also doubled to make one equal bet for each of the two one card hands. After the split, the player is automatically given second card in each hand to form two 2-card hands. If the player splits a pair of aces, only one more card is given to each hand (under standard rules). If the player splits any other pair, he can choose to hit, stand, or double on each of the hands. A second split may be allowed as well if again one or both of the new two card hands compose a pair (depending on the rule variations of each casino and blackjack game).

3) When player has decided actions to each of his hand to the end (finally standing or busting on each hand) the bankers face down card is turned face up and banker draws more cards until having a sum of 17 to 21 (under standard rules) of busting his hand.

Rule Variations

There are many possible rule variations to standard rules:

Number of decks: The number of decks used can vary from 1 to 8 depending on the form of blackjack played.

Hit or stand on soft 17: Usually rules require the dealer to stand on all 17s (hard or soft total). Some rule variations require the dealer to stand on a “hard” 17, but hit a “soft” 17.

Peek for blackjack: Under standard rules, the dealer peeks for blackjack when an ace or 10-point card is showing. Under some rules, dealer does not peek for blackjack.

Doubling: Typical online rules allow players to double on any two cards. Some variations limit doubling on hard sums of 9 to 11, and not on soft sums including an ace. Possibility to double on any two cards favors the player.

Surrendering: Some blackjack forms give player an option to surrender and lose half of the bet at the start of the hand (after 2-card hand is dealt). The surrender option is typically given after the dealer checks for blackjack, which is called a “late surrender.” A few game variations offer an “early surrender” before the dealer checks for blackjack.

Charlie: 7-card Charlie is a hand composed of 7 cards without busting. If this rule is in use, player´s hand is considered as an automatic winner. Other Charlie rules might also be rarely available.

Re-splits: After splitting your cards to form two separate hands, you may draw a matching card again and wish to split again. Some variations allow this, others do not. Some variations allow certain amount of resplits only. Usually re-splitting aces is not allowed, but rarely it is.

Hitting split aces: Under standard rules, player is only allowed to draw a single card to split aces. Some rare variations allow you to draw multiple cards to split aces.

Side bets: Some blackjack games offer an optional side bet, which pays if the player’s hand contains a certain combination of cards. For example, if players hand is 7-7-7. You might want to take a side bet for fun, but when played using optimal strategy, side bet is a –EV choice. Exceptionally high progressive jackpot might make a difference to this rule of thumb.

House Edge and Optimal Strategy

Blackjack usually has a house edge of ~0.5%. Optimal strategy for different online casino softwares and game variations are listed below in the table. House edge assumes using optimal strategy listed in the link for each variation. You can also use blackjack strategy tool yourself to get optimal strategy for different rule variations (rules are always listed somewhere on the casino homepage or software). Following house edges have been calculated using general guidelines available at Wizard of Odds and using Winner Gambling´s team´s unique programmed blackjack simulator, which simulates millions of hands of BJ using different rule variations.

Bet Sizing and Variance

Blackjack has pretty low variance. It has standard deviation of about ~1.15 per unit wagered. There are only a few casino games with this low variance, like roulette (1:1 bets), pai gow and baccarat. Still, with large bet sizes, variance is a huge factor when wagering for example toward bonus requirements. See casino software reviews for more info about the game speed with different softwares.

My last post was about some common mistakes when bettingor gambling, even with a basic understanding of probability. This post is going totalk about the other side: optimal betting strategies using some veryinteresting results from some very famous mathematicians in the 50s and 60s.I'll spend a bit of time introducing some new concepts (at least to me), setting up theproblem and digging into some of the math. We'll be looking at it from thelens of our simplest probability problem: the coin flip. A note: I will not becovering the part that shows you how to make a fortune -- that's an exercisebest left to the reader.


Background

History

There is an incredibly fascinating history surrounding themathematics of gambling and optimal betting strategies. The optimalbetting strategy, more commonly known as the Kelly Criterion, was developed in the 50s byJ. L. Kelly , a scientistworking at Bell Labs on data compression schemes at the time. In 1956, he madean ingenious connection between his colleague's (Shannon) work on information theory,gambling, and a television game show publishing his new findings in a papertitled A New Interpretation of Information Rate (whose original title wasInformation Theory and Gambling).

The paper remained unnoticed until the 1960s when an MIT student named Ed Thorptold Shannon about his card-counting scheme to beat blackjack. Kelly's paperwas referred to him, and Thorp started using it to amass a small fortune usingKelly's optimal betting strategy along with his card-counting system. Thorpand his colleagues later went on to use the Kelly Criterion in othervaried gambling applications such as horse racing, sports betting, and even thestock market. Thorp's hedge fund outperformed many of his peers and it wasthis success that made Wall Street take notice of the Kelly Criterion. There is agreat book called Fortune's Formula 1 that details the stories andadventures surrounding these brilliant minds.

Surely, Almost Surely

In probability theory, there are two terms that distinguish very similarconditions: 'sure' and 'almost sure'.If an event is sure, then it always happens. That is, it is not possible forany other outcome to occur. If an event is almost sure then it occurs withprobability 1. That is, theoretically there might be an outcome not belonging tothis event that can occur, but the probability is so small that it's smallerthan any fixed positive probability, and therefore must be 0. This is kind ofabstract, so let's take a look at an example (from Wikipedia).

Imagine we have a unit square where we're randomly throwing point-sized darts thatwill land inside the square with a uniform distribution. For the entire square(light blue), it's easy to see that it makes up the entire sample space, so we wouldsay that the dart will surely land within the unit square because there is noother possible outcome.

Optimal

Further, the probability of landing in any given region is the ratio of itsarea to the ratio of the total unit square, simplifying to just the area of agiven region. For example, taking the top left corner (dark blue), whichis 0.5 units x 0.5 units, we could conclude that (P(text{dart lands indark blue region}) = (0.5)(0.5) = 0.25).

Now here's the interesting part, notice that there is a small red dot in theupper left corner. Imagine this is just a single point at the upper leftcorner on this unit square. What is the probability that the dart lands on thered dot? Since the red dot has an area of (0), (P(text{dart landson red dot}) = 0). So we could say that the dart almost surely does not landon the red dot. That is, theoretically it could, but the probability of doingso is (0). The same argument can be made for every point in the square.

The dart actually does land on a single point of the square though, so eventhough the probability of landing on that point is (0), it still doesoccur. For these situations, it's not sure that we won't hit that specificpoint but it's almost sure. A subtle difference but quite important one.

StrategyBetting


Optimal Betting 2

Optimal Betting with Coin Tossing

Imagine playing a game with an infinite wealthy opponent who will always takean even bet made on repeated independent tosses of a biased coin.Further, let the probability of winning be (p > frac{1}{2}) andlosing be (q = 1 - p)3, so we have a positive overall expected valuefor the game 4. You start with (X_0) of initialcapital. Question: How much should we bet each time?

Example 1:

This can be made a bit more concrete by putting some numbers to it.Let's say our coin lands on heads with a chance of (p=0.53),which means tails must be (q=1-p=0.47). Our initial bankroll is(X_0=$100,000). How much of this ($100,000) should we bet on the firstplay?

Let's formalize the problem using some mathematics. Denote our remaining capitalafter the k'th toss as (X_k) and on the k'th toss we can bet (0leq B_k leq X_{k-1}). Let's use a variable (T_k = 1) if thek'th trial is a win, and (T_k=-1) for a loss. Then for the n'th toss, we have:

begin{align*}X_n &= X_{n-1} + T_nB_n &= X_{n-2} + T_{n-1}B_{n-1} + T_nB_n &= ldots &= X_0 + Sigma_{k=1}^{n} T_kB_k tag{1}end{align*}

One possible strategy we could use is to maximize the expected value of(X_n). Let's take a look at that:

begin{align*}E(X_n) &= E(X_0 + Sigma_{k=1}^{k} T_kB_k) &= X_0 + Sigma_{k=1}^{k} E(B_kT_k) &= X_0 + Sigma_{k=1}^{k} (p - q) E(B_k) tag{2}end{align*}

Since (p - q > 0) this will have a positive expected payoff. To maximize(E(X_n)), we should maximize (E(B_k)) (this is the only variable wecan play with), which translates to betting our entire bankroll at each toss.For example, on the first toss bet (B_0 = X_0), on the second toss (if we wonthe first one) bet (B_1 = 2X_0) and so on. It doesn't take amathematician to know that is not a good strategy. Why? The probability ofruin is almost sure (ruin occurs when (X_k = 0) on the k'th toss).

If we're betting our entire bankroll, then we only need one loss to lose allour money. The probability of ruin is then (1 - p^n) for (n) tosses (everyoutcome except winning on every toss). Taking the limit as (n) approaches infinity:

begin{equation*}lim_{n rightarrow infty} (1 - p^n) = 1 tag{3}end{equation*}

So we can see that this aggressive strategy is almost surely 5 going to result in ruin.

Another strategy might be to try and minimize ruin. You can probably already intuitthat this strategy involves making the minimum bet. From Equation 2, this isnot desirable because it will also minimize our expected return. This suggests that wewant a strategy that is in between the minimum bet and betting everything (duh!).The result is the Kelly Criterion.

The Kelly Criterion

Since our maximum bet is limited by our current bankroll, it seems plausible thatthe optimal strategy will always bet relative to our current bankroll. Tosimplify the math, we assume that the money is infinitely divisible. However,it should be noted that this limitation doesn't really matter too much when ourcapital is relatively large compared to the minimum divisible unit (thinkmillions vs. cents).

If on every toss, we bet a fraction of our bankroll (known as 'fixed fraction'betting), (B_k = fX_{k-1}), where (0 leq f leq 1), we canderive an equation for our bankroll after (S) successes and (F) failuresin (S+F=n) trials:

begin{equation*}X_n = X_0(1+f)^S(1-f)^F tag{4}end{equation*}

Notice that we can't technically ever get to (0) but practically there is a minimumbet and if we go below it, we are basically ruined. We can just re-interpretruin in this manner. That is, ruin for a certain strategy is when we willalmost surely go below some small positive integer (epsilon) as thenumber of trials (n) grows i.e., (lim_{nrightarrow infty}P(X_nleq epsilon) = 1).

Now let's setup what we're trying to maximize.We saw that trying to maximize the expected return leads us to almost surelyruin. Instead, Kelly chose to maximize the expected exponential growth rate.Let's see what that means by first looking at the ratio of current bankroll toour starting bankroll:

begin{align*}frac{X_n}{X_0} &= e^{log(frac{X_n}{X_0})} &= e^{n log(frac{X_n}{X_0})^{1/n}} &= e^{n G(f)} tag{5}end{align*}

So (G(f)) represents the exponent (base (e)) on how fast ourbankroll is growing. Substituting Equation 4 into (G(f)):

begin{align*}G(f) &= log(frac{X_n}{X_0})^{1/n} &= log((1+f)^S(1-f)^F)^{1/n} &= frac{1}{n}log((1+f)^S(1-f)^F) &= frac{S}{n}log(1+f) + frac{F}{n}log(1-f) tag{6}end{align*}

Now since (G(f)) is a random variable, we want to maximize the expectedvalue of it (which we denote as (g(f))):

begin{align*}g(f) &= E[G(f)] &= E[frac{S}{n}log(1+f) + frac{F}{n}log(1-f)] &= E[frac{S}{n}]log(1+f) + E[frac{F}{n}]log(1-f) &= plog(1+f) + qlog(1-f) tag{7}end{align*}

The last line simplifies because the expected proportion of successes andfailures is just their probabilities 6. Now all we have to do is a simpleexercise in calculus to find the optimal value (f^*) that maximizes (g(f)):

begin{align*}g'(f) = frac{p}{1+f} + frac{q}{1-f} &= 0 frac{p-pf+q+qf}{(1+f)(1-f)} &= 0 frac{1-(p-q)f}{(1+f)(1-f)} &= 0 && text{since } p+q=1 1 - (p-q)f &= 1 - f^2 f^2 - (p-q)f &= 0 f = f^* &= p - q && text{since } f>0 tag{8}end{align*}

So we now have our optimal betting criterion (for even bets), fractional betswith (f^*=p-q).

Another interesting behavior of varying our fractional bets can be gleaned bygraphing (G(f))7:

We can see that our (f^*) maximizes the growth rate. However, there is a point(f_c) where our growth rate becomes negative. This implies that if weover-bet (f > f_c), we will almost surely reach ruin (because we have anegative growth rate). The following (summarized) theorem from Thorp's paperstates this more precisely:

Theorem 1

  1. If (g(f) > 0), then (lim_{nrightarrow infty}X_n = infty) almost surely.

  2. If (g(f) < 0), then (lim_{nrightarrow infty}X_n = 0) almost surely.

  3. Given a strategy (Theta^*) and any other 'essentially different strategy' (Theta), we have (lim_{nrightarrow infty}frac{X_n(Theta^*)}{X_n(Theta)} = infty) almost surely.

From this theorem, we can see that if we pick a fraction such that (g(f)> 0), then we'll almost surely tend towards an increasing bankroll.Conversely, if we pick a fraction (g(f)<0), then we will almost surelyresult in ruin. This matches up with our intuition that over-betting iscounter-productive.

Example 2:

(Continued from Example 1)Suppose we have our even-bet coin toss game and the probability of heads is(p=0.53) and probability of tails is (q=0.47). Our initialbankroll is ($100,000) (big enough that the minimum bet isn't reallysignificant). Applying our optimal betting criteria, on our first playwe should bet (f=p-q=0.53-0.47=0.06) or (6%) of our bankroll, translating to($100,000 * 6% = $6,000). Assuming we win the first play, we should bet($106,000 * 6% = $6,360) and so on.

If we bet less than (6%), we will still be increasing our bankroll but not atthe optimal rate. We can also bet more than (6%) up to the theoretical point (f_c)such that (g(f_c)=0) with the same result.We can numerically determine this turning point, which in this case is(f_c approx 0.11973). So betting more than roughly 11.9% will almostsurely cause us ruin.

We can also compute the expected exponential growth rate using our optimal(f^*= 0.06):

begin{align*}g(f^*) = g(0.06) &= E[plog(1+f) + qlog(1-f)] &= 0.53log(1+0.06) + 0.47log(1-0.06)] &approx 0.001801 tag{9}end{align*}

So after (n) plays, a player can expect his bankroll to be(e^{0.001801n}) times larger. A doubling time can be computedby setting (e^{0.001801n}=2), resulting in (napprox 385) plays.

Betting with Uneven Payoffs and Other Variations

We've so far only looked at games with even payoffs. We can generalize this result.If for each unit wagered, you can win (b) units, we can derive a modified versionof Equation 7:

begin{equation*}g(f) = E[log(frac{X_n}{X_0}) = plog(1 +bf) + qlog(1-f) tag{10}end{equation*}

Solving for the optimum yields (f^*=frac{bp-q}{b}).

Another variation is when you can make multiple simultaneous bets such as whenmultiple players share a single bankroll. Going through a similar exercise, wecan derive values for (f_1^*, f_2^*, ldots) assuming the games playedare independent. When two players are playing the same game (e.g. same tablefor Blackjack), the bets are correlated and adjustments must be made.Additionally, we can analyze more complex situations such as continuous (ornearly continuous) outcomes like the stock market which require a more thoroughanalysis using more complex math. See Thorp's paper for more details.


Conclusion

Kelly's optimal betting criterion is an incredibly interesting mathematicalresult. However, perhaps what is more interesting is that this theoretical resultwas put into practice by some of the very mathematicians that worked on it!Thorp has had wild success applying it in various situations such assports betting, Blackjack and the stock market. Of course by itself thecriterion isn't much use, it is only once you've found a game that has apositive expected value that you can put it to use. I would go into how to dothat but I think I've written enough for one day and as I said, it's best leftas an exercise to the reader.


References and Further Reading

  • The Kelly Criterion in Blackjack Sports Betting, and the Stock Market by Edward O. Thorp.

  • Optimal Gambling Systems for Favorable Games, E. O. Thorp, Review of the International Statistical Institute Vol. 37, No. 3 (1969), pp. 273-293 .

  • William Poundstone, Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street. 2005. ISBN 978-0809045990. See also a brief biography of Kelly on William Poundstone's web page.

Optimal Craps Betting Strategy


1

William Poundstone, Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street. 2005. ISBN 978-0809045990. See also a brief biography of Kelly on William Poundstone's web page.

Blackjack Betting Guide

2

Best Blackjack Betting Strategy Reddit

This whole section just basically summarizes (with a bit more step-by-step for the math) the paper 'The Kelly Criterion in Blackjack Sports Betting, and the Stock Market'. So if you're really interested, it's probably best to check it out directly.

3

It doesn't really matter if the bias is heads or tails. The point is that you get to pick the winning side!

4

The expected value of winning for bet (B) is (Bp-Bq = B(p-q) > 0) since (p > q).

5

Almost surely here because it's theoretically possible that you can keep winning forever but it's such a small possibility that it basically can't happen. This is analogous to the red dot in the unit square.

6

The expected value of a binomial distribution (e.g. coin tossing) is just (np). So (np/n = p).

7

Image from 'The Kelly Criterion in Blackjack Sports Betting, and the Stock Market'.

⇐ ⇐ 40 Casino Avenue Apollo Bay
⇒ ⇒ Free Pai Gow Poker Download